Vidéos
LA CHAMBRE DU ROI
En 2003 nous avions publié sur les trames d'implantation de Gizeh et leur utilisation pour le concept de Khéops,
les rampes internes, le point de convergence, les triplets Pythagoriciens, etc,...(voir "
Les Contributions
").
Ceci avait fait l'objet de notre livre "Numerus, Le Concept de Gizeh".
L'ensemble de ces connaissances n'ayant pu surgir du néant nous avons durant quelques années tenté de mettre
en forme le parcours de la connaissance humaine en ces temps reculés.
Après de longues recherches, nous avons pu apporter des réponses au travers d'un second ouvrage,
"Les Deux Sycomores de Turquoise", histoire de la connaissance du Néolithique à nos jours de l'Atlantique au Nil.
Dans le même temps nous avons poursuivi nos recherches sur la pyramide de Khéops et les mathématiques objet d'un
troisième ouvrage intitulé "La Brique d'Imhotep" qui comporte de nombreuses réponses surprenantes et
cependant facilement vérifiables par chacun.
Extraordinaire Chambre du Roi
Contrairement à La Chambre de la Reine construite en calcaire la Chambre du Roi a été construite au moyen de blocs,
dalles et linteaux en granit parfaitement ajustés ce qui semble traduire une volonté de pérennité.
Ses dimensions sont très particulières, soit 10 coudées dans le sens Nord/Sud et 20 Coudées dans le sens Est/Ouest.
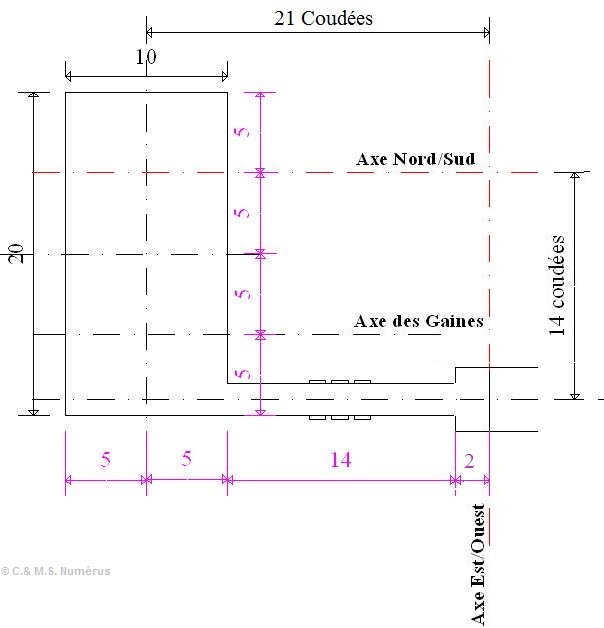
Quels sont les premières remarques?
Le triangle déterminé par la diagonale du sol de la Chambre du Roi peut constituer
la mesure de référence de la coudée royale:
Cette coudée Royale figure dans la Chambre du Roi en tant que 1/100 du périmètre du triangle rectangle dont les cotés sont 10 et 20, c'est à dire les dimensions des bases de
la Chambre du Roi.
Preuve:
La diagonale du rectangle de base est égale à la racine de la somme des carrés des côtés soit Racine de 500 = 22,360679
Le Périmètre du triangle sera donc 10 + 20 + 22,360679 = 52,360679 et 1/100 = 0,5236
[Note- mars 2018]: Il apparaît que cette relation 1/2 aurait été montrée en 1990 par MM. Claude Gruais et CLaude Mouny dont nous n'avions pas connaissance des travaux.
La coudée Royale est-elle une valeur absolue ou une proportion?
[Note- mars 2018]: Nous avons développé cette question en février 2011 sur le forum ainsi que dans notre livre "La Brique d'Imhotep"
sous-titré "Les mathématiques dans la Pyramide de Khéops, l' une des clés pour
en approcher sa magnificence."
(ISBN: 978-2-9531305-2-2, février 2012, Non publié en raison de nos recherches en cours), puis dans le premier chapitre de notre livre "Khéops,Le Livre de Pierres"
publié en 2015.
On pourra également remarquer que les valeurs 7 et 11 sont bien présentes par rapport aux axes de la Pyramide
ou de la grande descenderie: 21 (10 plus 11) et 14 (2 fois 7).
Ces valeurs 7 et 11 sont constitutives de la Pyramide de Khéops (hauteur 280, soit 7 fois 40 et base 440 soit 11
fois 40) mais on notera surtout qu'elles font partie du premier
triplet Pythagoricien 7-11-13 
que nous avions montré antérieurement. (Faux triplet Pythagoricien au regard de nos actuelles connaissances mais exact
en regard des méthodes graphiques qui devaient avoir cours à l'époque).
[Note]: la Pyramide de Khéops et la chambre du Roi en particulier utilisent simultanément les deux premiers
triplets 7-11-13 et 11-13-17 ainsi que nous le montrons dans notre livre "La Brique d'Imhotep" au moyen des séquences
du dallage du sol de la chambre du Roi.
Nous sommes en présence d'un parallélépipède rectangle que nous avons nommé "Brique d'Imhotep" par opposition à ce que nos
actuels mathématiciens nomment une "Brique de Pythagore", cette dernière comportant beaucoup moins de propriétés
mathématiques que celle d'Imhotep.
(Imhotep peut en être considéré comme l'Architecte dans le sens où les particularités architectoniques rattachent la Pyramide de Khéops à celle de Djoser à Saqqarah puis à
celles de Snéfrou à Dahchour.
Le vizir Hémiounou, -Fils de Néfermaât frère de Khéops et Petit-fils de Snéfrou-, en aurait conduit la réalisation débutée sous le règne de son oncle Khéops.
La transmission des connaissances semblerait ainsi avoir suivi la lignée familiale.)
Beaucoup se sont interrogés sur le fait inhabituel pour les concepteurs d'utiliser une valeur fractionnaire 11,18 pour
la hauteur de la chambre du Roi même si ils avaient bien vu que cela permettait d'obtenir
différents triangles Isiaques (ou triplets Pythagoriciens ou triangles 3-4-5) tel le 15-20-25.
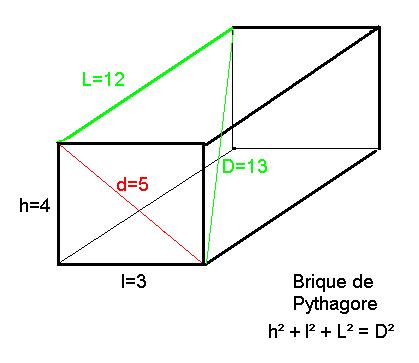
De fait la Brique de Pythagore ne répond qu'à une seule équation mathématique (h² + l² + L² = D²) en 2 dimensions (dans un même plan) alors que celle d'Imhotep
en utilise deux simultanément, en 2 et 3 dimensions, (dans un plan et en volume).
Soit pour la Chambre du Roi:
h=11,18
l=10
L=20
D=25
Avec lesquels nous obtenons:
11,18 = Racine de(100 + 400)/2 et simultanément 125 + 100 + 400 = 625 ,d
La Brique de Pythagore n'utilise pour sa part que la seconde: h² + l² + L² = D²
Ce qui précède en est un aperçu.
Interessons nous maintenant au dallage du sol:
Le dallage est constitué de 20 dalles de granit parfaitement ajustées réparties sur 6 rangs avec alternativement pour chacun de ceux-ci une dalle de largeur du rang avec
pour longueur 1.
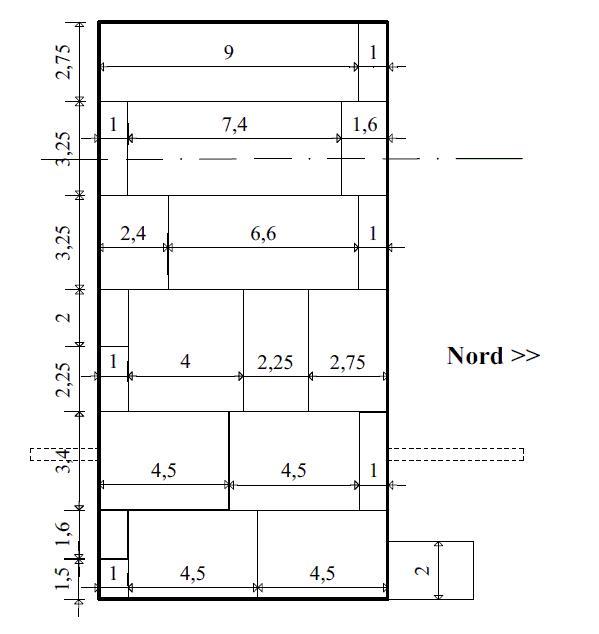Remarque1: Lorsque l'on sait que le plafond est constitué de 9 linteaux monolitiques pesant plusieurs
tonnes chacun on admettra qu'ils maîtrisaient parfaitement la technologie de la manutention et que ce n'est donc
pas pour une question de mise en oeuvre que le sol a été fractionné en 20 dalles avec une telle perfection de taille!...
Remarque2: Dans ce qui suit nous verrons que les dimensions de ces dalles correspondent à une réalité mathématique
rigoureuse que le tailleur de pierres d'Assouan ou d'ailleurs ignorait et que cela ne pourrait être le fruit du hasard.
Simplement un exemple:
Le second triplet 11-13-17 est bien présent dans le dallage du sol de la chambre du Roi car
les largeurs des 4 premiers rangs côté Ouest où se situe le sarcophage lui correspondent directement :
Rang N°1 largeur 2,75 = 11 /4
Rang N°2 largeur 3,25 = 13 /4
Rang N°3 largeur 3,25 = 13 /4
Rang N°4 largeur 4,25 = 17 /4
Un autre exemple pour conclure ce bref aperçu:
Le sarcophage a été déplaçé au cours des siècles, mais on peut lui supposer une situation initiale cohérente...
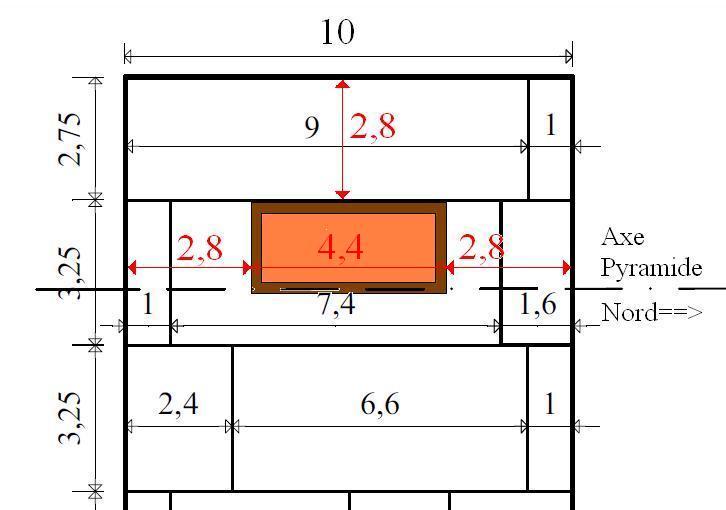
On peut observer que le sarcophage mesure 4,4 coudées (2,29 mètres) par 1,9 coudée.
La chambre du Roi mesurant 10 coudées, si un positionnement en symétrie avait été recherché, cela aurait conduit
à le placer à 2,8 coudées de chacun des murs Nord et Sud (2,8+4,4+2,8 = 10).
Mais... 2,8 et 4,4 ne serait-ce pas un rapport de 100 avec la Pyramide qui mesure pour sa part 280 coudées par 440 ?
Dans ce cas rien ne s'opposerait à positionner le sarcophage également à 2,8 coudées de la face Ouest, ce qui
aurait pour autre avantage de l'inclure totalement sur la dalle N°'4 attendu que la largeur de la dalle N°2 qui est
de 2,75 coudées l'éloigne d'autant de cette face Ouest.
Ce, sans qu'il y ait pour autant chevauchement de joints au sol.
Ceci n'est qu'une simple hypothèse de notre part, mais qui n'avait sans doute pas échappé aux yeux des concepteurs!
Cette chambre du Roi comme tout l'ensemble de Gizeh est mathématiquement somptueux et si l'on veut un lien entre
Khéops et Képhren, on pourra remarquer que la base de Képhren est de 410. Ne serait ce pas en rapport avec 11-13-17?
(11+13+17 = 41).
Nous avons collationné en 20 ans, (mais surtout étudié), beaucoup de nombres ou valeurs qui se rapportent à Gizeh.
Nous croyons peu à l'usage de valeurs absolues mais davantage à un système de proportions qui "s'emboîtent"
parfaitement les unes dans les autres et qui s'inscrivent rigoureusement dans le courant des recherches mathématiques
qui prenaient place il y a 4.500 ans. (A ce sujet, se référer aux tablettes cunéiformes dites Plimpton 322).
|