ATTENTION!!
Ce site NE PEUT PAS fonctionner correctement car Javacript n'est pas activé sur votre navigateur.
(Menu ou diverses fonctions inactives...)
Pour informations,
Cliquez ici.
|
Vidéos
LE CONCEPT MATHEMATIQUE DE KHéOPS
| Pour les résumés rapides en vidéos, cliquez sur l'image. |
Tout ceci peut-il être le
résultat du hasard?
On peut constater que chaque élément
de l'ensemble correspond à l'utilisation d'un rapport
de proportions simple tels que 1/1, 1/2, 2/3, 7/9, etc,. . .
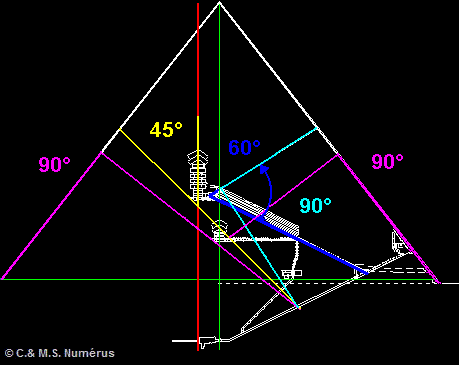
Quid des angles très particuliers que l'on
a pu également constater tels que
45°,60°,90° ou encore des
perpendicularités entre différents
éléments?
Examinons la géométrie des gaines :
. . .qui ne sont pas symétriques pour la chambre
du Roi dont l'axe vertical est décalé de 21
coudées mais qui débouchent sensiblement
à un même niveau externe.
Pour la gaine sud de la chambre de la Reine, le robot
Upuhaut a mesuré une pente moyenne de 39
degrés et 60 centièmes ou 39 degrés et
36 minutes. La pente des faces extérieures de la
pyramide est d'environ 51 degrés 25. La somme des
deux serait donc de 90 degrés. Pouvons nous en
conclure que la volonté architecturale était
qu'elles soient respectivement perpendiculaires ou que cela
résulte de la mise en oeuvre du rapport 7/9 avec
usage des trames de construction ? (Dans ce cas l'angle
serait de 89° 17 minutes, les 51°25' de la pente
externe plus le s37°52' du rapport 7/9 de la gaine
Sud).
Mais nous pouvons surtout dire que la pente de cette
gaine qui si elle était prolongée
correspondrait dans un même plan à un point de
la grande descenderie que j'ai nommé "
Le Point de Convergence
" qui serait l'origine du triangle rectangle
construisant le rapport 7/9.
La gaine sud de la chambre Royale a pour sa part
été mesurée pour avoir une pente de 45
degrés. Ce n'est pas neutre non plus. Si cette gaine
était prolongée elle serait
nécessairement en intersection avec la
précédente et je montrerai que ce ne sera pas
en un point quelconque.
Quant à la gaine nord de la Chambre Royale,
donnée pour une pente d'environ 33 degrés 30
minutes, elle fera donc nécessairement un angle de 60
degrés avec la grande galerie qui elle-même a
une pente de 26 degrés 30 minutes. (La grande galerie
a été réalisée en utilisant le
rapport de 1/2 qui génère un angle absolu de
26 degrés et 33 minutes).
Enfin je montrerai également que la droite
élevée depuis le Point de Convergence vers la
gaine nord de la Chambre Royale à l'intersection de
la gaine et l'axe vertical de la Pyramide où se situe
le sommet de la grande galerie formera un angle de 90
degrés.
La gaine nord de la chambre de la Reine qui n'est pas
rectiligne n'a été que partiellement
explorée mais semble symétrique de la gaine
sud et formerait donc également un angle de 90
degrés avec la pente extérieure de la
pyramide. (Pour ce dernier cas, il ne s'agit que d'une
hypothèse basée sur la symétrie avec la
gaine sud).
Ces angles étaient-ils un objectif de
construction ou à contrario une conséquence
et par la même une confirmation de la
méthode utilisée? De mon point de vue je
souscris à la seconde hypothèse comme je vais
tenter de le montrer.
Les concepteurs connaissaient parfaitement les triangles
rectangles et les rapports qui les régissent comme je
l'ai déjà montré avec l'utilisation des
triangles 7-11-13, 11-13-17, 41-53-67.
Et bien que procédant sans doute au moyen d'un
recherche expérimentale plus physique que
théorique, une propriété
particulière qui régit les hypoténuses
des triangles rectangles ne leur avait pas
échappée!
J'ai pris soin de formaliser et démontrer cette
propriété que vous pouvez consulter
en cliquant ici
En utilisant cette propriété on aboutit
exactement à ce que l'animation montre.
Si je fais également état de l'existence de
ce que j'ai nommé "Le point de convergence"
(Pour la démonstration mathématique de son
existence,
cliquez ici
, tout architecte, chef de chantier ou conducteur de
travaux comprendra immédiatement que c'est avec et
à partir de ce type de lieu que, sans les moyens dont
nous disposons de nos jours, qu'il est possible de
contrôler avec exactitude la précision et la
qualité d'une mise en oeuvre au moyen de simples
visées!
On pourra également remarquer que l'intersection
de la grande Galerie et de la grande descenderie constitue
un autre point de visée.
La situation de ces points de visées laisse
supposer qu'ils auraient été destinés
à contrôler des éléments
essentiellement situés dans le volume Sud de
la Pyramide.
Ceci aide également à comprendre que
l'ensemble des éléments de la construction
donnent l'impression d'une "vague" partant du Nord et
montant vers le Sud.
Les très nombreuses particularités mathématiques de la Pyramide de Khéops suffisent à démontrer qu'elles ne peuvent être le fruit du hasard mais qu'au contraire elles résultent de
connaissances certaines des concepteurs et de la méthodologie mise en oeuvre.
Indépendamment de ce que vous pouvez consulter sur ce site, (et en particulier
"La Chambre du Roi" 
), vous trouverez ci-dessous 11 pages du chapitre 6 du livre "La Brique d'Imhotep" qui en fournit différents exemples...
Souvenez vous seulement que l'ancienne Egypte ne disposait pas d'ordinateurs et que le dessin demeurait vraisemblablement leur outil de base...
Page Précédente du Livre
|
|
Page Suivante du Livre
|
|
|
|
|
| Accueil |
Page Précédente |
Haut de Page |
Site optimisé pour affichage 1024 x 768 pixels.
Droits de reproduction et de diffusion réservés. Copyright© C. & M.Sélaudoux 2003-2025
Data Center - WD28net Odessa 65069 UA -
27690
|
|