Pour donner un simple aperçu de mon propos il suffit de savoir que les Babyloniens recherchaient déjà sur ce qui plus tard deviendra " les triplets pythagoriciens ".

Ceci est inscrit dans les tablettes cunéiformes dites " Plimpton 322 ", qui regroupent plus de quinze triplets pythagoriciens, et qui sont conservées aux USA à l'université de Columbia.

La question de cette relation entre les nombres s'est poursuivie jusqu'à nos jours, et Pierre de Fermat l'a reprise en 1621 dans sa fameuse conjecture, dite grand théorème (ou dernier théorème) de Fermat, qui énonce que si n est supérieur à 2, il n'existe pas d'entiers x, y et z non nuls pour lesquels :

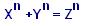
Les mathématiciens du monde entier pendant trois siècles ont procédé à des recherches sur cette question et au 19ème siècle une forte récompense fut promise par l'Académie des Sciences.

C'est ainsi que la constante de ces recherches au cours desquelles les pyramides furent conçues peut se lire tout simplement au travers du nom de tous les grands mathématiciens qui ont eu a poursuivre ce courant, et je ne citerai parmi ceux-ci que quelques uns :

Après les Babyloniens, la chaîne se poursuit avec Thalès et Pythagore vers -500 av. J.C., Diophante d'Alexandrie -350 av. J.C., Euclide -200 av. J.C., Pierre de Fermat, Euler, Gauss jusqu'à Andrew Willes, et de nombreuses recherches se poursuivent encore de nos jours sur les relations entre les nombres premiers par exemple(*).

L'oeuvre de Diophante d'Alexandrie "Les arithmétiques" comportant treize livres, ainsi que les six premiers livres des "Eléments d'Euclide" furent traduits au 16ème siècle à l'université d'Heidelberg par le célèbre linguiste et philosophe allemand Wilhelm Holtzmann, dit Xylander, (1532-1596), puis complétée et commentée en France, en latin, par Bachet de Méziriac (1621).

Imhotep, reconnu pour être le plus grand savant de l'Egypte Antique n'a certes pas pu ignorer cette question commencée bien avant lui et qui a perduré plusieurs millénaires !

(*) Note: Thomas Nicely (Professor of Mathematics Lynchburg College Virginia U.S.A.), est un mathématicien qui travaille dans le domaine de la théorie des nombres.
Il s'intéresse en particulier aux nombres premiers " jumeaux ".C'est-à-dire aux nombres premiers dont la différence vaut 2. Exemples : 5 et 7, 11 et 13...
En septembre 1994, Il constate que les calculs effectués sur l'un de ses ordinateurs donnaient un résultat différent qu'avec d'autres machines.
L'ordinateur en question était équipé du nouveau processeur Pentium d'Intel.
Le mathématicien découvre alors que le nouveau processeur Intel Pentium donnait un résultat incorrect lors du calcul de 1/824633702441.
(Ce nombre apparaissait dans ses calculs car 824633702441 et 824633702443 sont jumeaux).
C'est ainsi que fut découvert et communiqué le " Bug " du Pentium le 19 octobre 1994.

Accueil	Page Précédente	Haut de Page