ATTENTION!!
Ce site NE PEUT PAS fonctionner correctement car Javacript n'est pas activé sur votre navigateur.
(Menu ou diverses fonctions inactives...)
Pour informations,
Cliquez ici.
|

Vidéos
LA HAUTEUR DE KHéOPS, UN CHOIX EXTRORDINAIRE
Pour comprendre aisément les Pyramides, il est indispensable d'utilser leurs propres unités de mesures, essentiellement la Coudée Royale de Memphis qui correspond à 0,5236 de nos mètres, soit 52,36 centimètres et dont le symbole est Cr.

La Règle de l'Architecte de l'Egypte Antique.
La valeur de 280 coudées résulte de 10 fois le nombre 28 , lui même base de la divison de la règle de l'Architecte.
Le nombre 28
C'est un entier parfait:1+2+4+7+14 = 28
C'est la somme des 8 premiers entiers: 0+1+2+3+4+5+6+7 =28
C'est la somme des premiers entiers naturels: 1+2+3+4+5+6+7 = 28
C'est la somme des 5 premiers nombres premiers: 2+3+5+7+11 =28
C'est la somme des 5 premiers nombres NON premiers: 1+4+6+8+9 = 28
Sans même avoir besoin d'aller dans la lune et le cycle lunaire, le constat est là: il ne s'agit pas d'un nombre choisi au hasard...
Les rapports 1/2 et 2/3
Le rapport 1/2,"la moitié de " est fondamental et omniprésent, de même que le rapport 1/4 qui est la moitié du rapport 1/2 et encore 3/4 somme de trois fois 1/4.
Rien de bien compliqué donc.
Par exemple la chambre du Roi (ou chambre haute) est la seule a être construite en granit pour en assurer la pérennité.
Sa largeur de base est exactement 10Cr et sa longueur 20Cr ce qui lui permet d'être le conservateur étalon de la valeur de la
"Coudée Royale(Cr)"
Le rapport 1/3,"le tiers de " est lui ausssi omniprésent, de même que le rapport 2/3 qui est la somme de 1/3+1/3.
Ce "système" de proportions se démontre par comment il a été procédé au choix des
lieux d'implantations des trois grandes pyramides.
des trois grandes pyramides.
Cela malgré que pendant des décennies une infinité de publications qui n'aboutissaient pas rigoureusement alors que la réponse est extrêmement simple et ne nécessite aucune connaissance particulière.
Extra-terrestres, racines carrées,pi, phi, constellations célestes ne sont pas nécessaires.
Proportions des pyramides
Heureusement que l'Egypte Antique ne connaissait pas la division, et que pour calculer ses proportions, elle avait inventé les Fractions Egyptiennes.
 © Reproduction interdite sans autorisation.
© Reproduction interdite sans autorisation.
En bref, et un exemple va suivre, ces fractions constituent une somme de fractions dont le numérateur est égal à 1 et le dénominateur un entier positif, parfois nommé "un développement de Fractions Egyptiennes"
résultant de la décomposition du rapport de deux entier dont le numérateur est inférieur au dénominateur.
Deux fractions identiques ne peuvent cependant se répéter dans le développement.
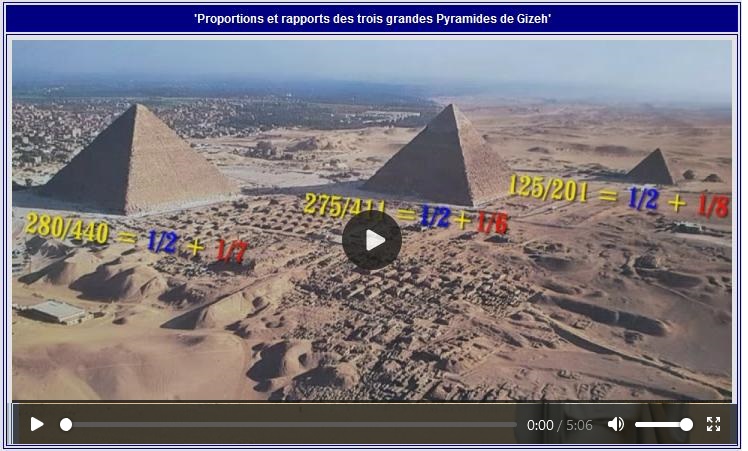
Exemple Khéops, avec ses dimensions de 280/440.
De nos jours, le résultat pour nous est 7/11 soit 0,636.364 et à quatre décimales: 0,6363que l'on peut considérer comme "proche de", mais pas exactement 2/3
Les deux dimensions sont décomposées en:
hauteur 280 divisible par 5 et 7
et pour la base 440 divisible par 5 et 11
Il en résulte donc le rapport de 7/11
Si l'on utilise les savoirs de l' Egypte Antique, le développement selon les Fractions Egyptiennes sera:
280/440 = 7/11 = +1/2+1/9+1/1.160
Ce même rapport 7/11 peut s'écrire d'une infinité de manières par exemple:
7/11 = +1/2+1/8+1/129+1/18.875
7/11 = +1/2+1/8+1/128
Pour l'Egypte Antique, Un règle d'arrondi consistait à réduire de 1 le dénominateur de la dernière fraction que l'on souhaitait conserver,
7/11 = +1/2+1/8+1/128
et nous obtenons:
7/11 = +1/2+1/7
Nous obtenons alors les résultats suivants:
De nos jours 7/11 est égal à 0,6363
et quatre millénaires auparavant 7/11 était déjà égal à 0,6363 ce qui confirme que l'Egypte Antique savait aussi bien calculer que nous mais avec des méthodes différentes.
( Nous attirons votre attention sur le fait que la base de Khéphren est mesurée pour 411 coudées, et non pas 410, comme pratiqué par l'usage courant de même pour Mykérinos la mesure réelle est de 201,44 coudées
et non pas 200 comme dans l'usage courant. Source: W.M.F.Petrie)
 © Reproduction interdite sans autorisation.
© Reproduction interdite sans autorisation.
Les Fractions Egyptiennes appliquées aux trois pyramides nous apportent un éclairage bien particulier sur la cohérence et les relations de l'ensemble!
Les Proportions...
Mises à jour 2015-2022:
Que peut-on constater également d"un simple coup d'oeil?
Que les trois pyramides avec des dimensions différentes sont toutes les trois chacune dans un même rapportde proportion très très voisin de 2/3 (0,666666) et que Khépren y répond très exactement alors que l'on serait plutôt enclin à
penser que Khéops détenait la perfection...
Encore plus interessant: les seuls compléments variables du rapport constant 1/2 sont constituées par 1/6, 1/7, 1/8, et là, à notre seul et modeste avis nous pensons qu'il s'agit là de l'objectif qui a determiné
les dimensions physiques des pyramides dans un rapport de proportion constant bien qu'avec une réalité physique du simple au double...
Nous résumons:
Hormis le "Pourquoi" des pyramides, pour ce qui est du "Comment" nous pouvons dire que:
Le choix des trois rapports de proportions, a été le premier acte fondateur des trois grandes pyramides de Gizeh,
Choix qui fut suivi par celui de leurs hauteurs,la hauteur clé initiale étant celle de Khéops: 10 fois le nombre parfait 28 hauteur à partir de laquelle le jeu des proportions déterminait tant la valeur de
sa prore base mais également les hauteurs et bases des deux autres.
Du rapport des deux précédents, il en est résulté la dimension de chacune des trois bases.
Ces valeurs des dimensions une fois établies conduisent ensuite au positionnement réciproque des pyramides tel que que nous l'avons explicité
en supra.
Ce système ne s'arrête pas là et pour, -en vous épargnant le calcul-, vous donner un exemple complèmentaire, considérons le rapport largeur Est-Ouest du rectangle périmètrique des pyramides1419. sur sa longueur Nord-Sud 1732
Selon nos mathématiques actuelles:
1419/1732 = 0,81928 qui selon nos actuelles règles d'arrondis doit s'écrire: 0,82
ou bien 1419/1732 = 71/87 =1/2+1/4+1/14 qui selon nos actuelles règles d'arrondis doit s'écrire: 0,819 et qui pouvait également s'écrire réduite à deux fractions egyptiennes: 1/2+1/3 =0,833
Sa diagonale par rapport à sa largeur s'écrira 1419/2239 soit 1/2+1/8+1/124 réductible en deux fracytions egyptiennes 1/2+1/7 = 0,642
Sa diagonale par rapport à sa longueur s'écrira 1732/2239 soit 1/2+1/4+1/44 qui peut réduite à deux fractions egyptiennes 1/2+1/3 = 0,833.
TOUT n'est QUE proportions pour ces trois pyramides. Vous venez d'en constater quelques unes..., il en existe bien d'autres en parfaite cohérence.
(Notre ami Pythagore n'avait-il pas dit que: "Tout est arrangé selon les nombres" ?).
Celui qui découvre Gizeh est en premier lieu interpellé, -outre le gigantisme-, par le fait que les trois pyramides sont semblables dans leurs proportions bien que possédant des dimensions différentes.
C'est cela qui conjugué avec l'absence d'alignement des trois pyramides peut induire un premier questionnement,
Khéops et son architecture mathématique en est un autre,
Khéphren ne s'est révélé à nos yeux que bien plus tard.
Si les trois pyramides sont dans un rapport proche de 2/3, Képhren est le seul à le posséder d'une façon parfaite: 1/2+1/6 c'est 0,666666....
Il comporte de plus les valeurs communes aux trois pyramides et l'un de nos regrets demeurera de ne pas l'avoir étudié davantage.
Cette pyramide nous laisse l'impression que notre esprit a été occupé par Khéops alors que comme le ferait la main d'un prestidigitateur, dans le même temps, c'est l'autre qui exécute le tour.
Mykérinos ne nécessite que deux nombres premiers, 2 et 5, alors que les valeurs des deux autres pyramides nécessitent l'usage des cinq nombres premiers.
Sa hauteur s'écrit 5x5x5 (Nous dirions une puissance au cube).
Sa base s'écrit : 2x2x2x5x5 (nous dirions aujourd'hui une puissance cubique par une puissance carrée).
Les proportions hauteurs/bases sont de 7/11 pour Khéops et 8/11 pour Mykérinos.
Et l'n pourra simplement remarquer que la hauteur de Mykérinos est dans le rapport 5/11 avec celle de Khéphren.
Ce que nous pouvons en vérité déduire est que:
- les pyramides nous conduisent aux questionnements
- il y a 4.500 ans, L'Egypte Antique disposait déjà d'une parfaite connaissance des nombres et proportions et avait constitué des méthodes fiables pour les utiliser,
- Ils l'ont inscrits dans la pierre pour en témoigner et les transmettre en sus de multiples autres connaissances
|

|

|

|
| Accueil |
Page Précédente |
Haut de Page |
Site optimisé pour affichage 1024 x 768 pixels.
Droits de reproduction et de diffusion réservés. Copyright© C. & M.Sélaudoux 2003-2026
Data Center - WD28net Odessa 65069 UA -
30
| |