ATTENTION!!
Ce site NE PEUT PAS fonctionner correctement car Javacript n'est pas activé sur votre navigateur.
(Menu ou diverses fonctions inactives...)
Pour informations,
Cliquez ici.
|

Vidéos
UN THéORèME
-Bien que ne l'ayant pas vu dans mes livres de
géométrie d'étudiant, un
théorème m'aurait certainement plu et aurait
par exemple pu s'énoncer comme ceci:
|
Lorsque deux triangles rectangles sont
semblables :
Si l'un des cotés de l'angle droit du
premier est perpendiculaire au coté
respectif de l'angle droit du second, leurs
hypoténuses seront soit perpendiculaires
entre elles soit formeront un angle égal
à la différence de la valeur des
angles non droits du triangle rectangle.
Si l'un des cotés de l'angle droit
du premier est perpendiculaire au coté non
respectif de l'angle droit du second, leurs
hypoténuses seront soit parallèles
entre elles soit formeront un angle égal
au double de la valeur de l'un quelconque des
angles non droits du triangle rectangle.
|
S'il n'a pas été formulé
précédemment alors ce sera le mien.
|
|
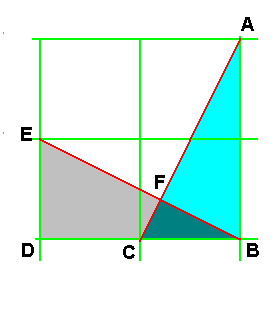
Exemple de démonstration
partielle:
Les triangles ABC et BDE sont deux
triangles rectangles égaux formés par
les diagonales de deux rectangles égaux
générés par une trame
constante. (Quelles que soient les dimensions des
rectangles si ceux ci sont égaux).
Les deux triangles rectangles ABC et BDE
sont égaux ayant leurs trois cotés
égaux.
Les angles CAB et EBD sont donc
égaux.
Dans les triangles ACB et FCB:
L'angle FCB est commun et l'angle FBC
égal à l'angle EBD lui même
égal à l'angle CAB.
Il en résulte que le triangle FCB
sera un triangle rectangle semblable aux deux
précédents, que l'angle CFB sera un
angle droit et les droites AC et EB
perpendiculaires entre elles.
|
La technique est très aisée à
mettre en oeuvre en utilisant les diagonales de rectangles
semblables générés par une trame de
valeur prédéterminée.. (Elle peut
également combiner des trames décalées
ou encore des rapports de valeurs différentes...).
Exemple: Si vous utilisez une trame
constituée de carrés égaux, les
diagonales (ou leur prolongement) de deux rectangles
égaux (constitués dans cet exemple du rapport
1/2 mais qui peut être n'importe lequel), ces
diagonales seront nécessairement dans les cas de
figure évoqués ci dessous.
|
|
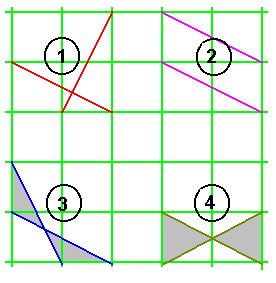
Les droites formées par les diagonales
des rectangles seront soit:
1- Perpendiculaires,
2- Parallèles,
3- Soit formeront un angle égal
à la différence de la valeur des
angles non droits du triangle rectangle.
4- Soit formeront un angle égal au
double de la valeur de l'un quelconque des angles
non droits du triangle rectangle.
|
Ma conclusion est que pour la conception de
Khéops, c'est manifestement la méthode qui a
été utilisée combinée avec
l'usage des rapports simples exposés dans ces pages,
eux mêmes basés sur l'usage des deux trames
décalées de 11...

|

|

|
| Accueil |
Page Précédente |
Haut de Page |
Site optimisé pour affichage 1024 x 768 pixels.
Droits de reproduction et de diffusion réservés. Copyright© C. & M.Sélaudoux 2003-2026
Data Center - WD28net Odessa 65069 UA -
321
|
|