ATTENTION!!
Ce site NE PEUT PAS fonctionner correctement car Javacript n'est pas activé sur votre navigateur.
(Menu ou diverses fonctions inactives...)
Pour informations,
Cliquez ici.
|

Vidéos
A THEOREM
Although not having seen it in my geometry student's
books. I would certainly have appreciated a theorem which
could have been stated like this for example:
|
When two right-angled triangles are similar:
If one side of the right angle of the first is
perpendicular to the respective side of the right
angle of the second, their
hypotenuses will be either perpendicular between
them or
will form an angle equal to the difference of the
value of the nonright angles of the right-angled
triangle.
If one side of the right angle of the first is
perpendicular to the nonrespective side of the
right angle of the second, their hypotenuses will be either
parallel between them or will form an
angle equal to the double of the value of the
unspecified one of the nonright angles of the
right-angled triangle.
|
If it was not previously formulated then it will be
mine. . .
|
|
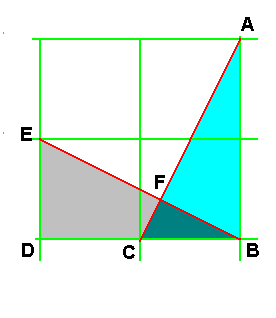
Example of partial demonstration:
Triangles ABC and BDE are two equal right-angled
triangles formed by the diagonals of two equal
rectangles generated by a constant layout sheet.
(Whatever dimensions of the rectangles if those are
equal).
The two right-angled triangles ABC and BDE are
equal their three having dimensioned equal.
Angles CAB and EBD are thus equal.
In triangles ACB and FCB:
Angle FCB is common and angle FBC equal to angle
EBD him even equal to angle CAB.
It results from it that triangle FCB will be a
right-angled triangle similar to the two
precedents, that angle CFB will be a right angle
and lines AC and EB perpendicular between them.
|
The technique is very easy to implement by using the
diagonals of similar rectangles generated by a lgrid of
predetermined value. (It can also combine avgrid shifted or
different values' ratios...).
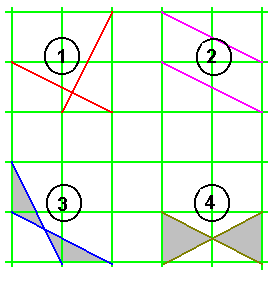
Example: If you use a layout sheet made up of
equal squares, the diagonals (or their prolongation) of two
equal rectangles (made up in this example of ratio 1/2 but
which can be any), these diagonals will necessarily be in
the evoked cases below.
|
|
The lines issued from the diagonals of the
rectangles will be:
1 - Perpendiculars,
2 - Parallels,
3 - Either will form an angle equal to the
difference of the value of the nonright angles of
the right-angled triangle.
4 - Either will form an angle equal to the
double of the value of the unspecified one of the
nonright angles of the right-angled triangle.
|
My conclusion is that for the design of Kheops, it is
obviously the method which was used combined with the use of
the simple ratios explained in these pages, themselves based
on the use of the two layout sheets of 20 cubits shifted of
11. . .

|

|

|
| Welcome |
Page Previous |
Top |
Site optimized for 1024 x 768 pixels.
Copyright© C. & M.Sélaudoux 2003-2024
|
|