ATTENTION!!
Ce site NE PEUT PAS fonctionner correctement car Javacript n'est pas activé sur votre navigateur.
(Menu ou diverses fonctions inactives...)
Pour informations,
Cliquez ici.
|
Vidéos
CHEOPS, THE MATHEMATICAL CONCEPT
All this can it be the result of the
chance?
One can note that each element of the unit
corresponds to the use of simple ratios such as 1/1, 1/2,
2/3, 7/9, etc..
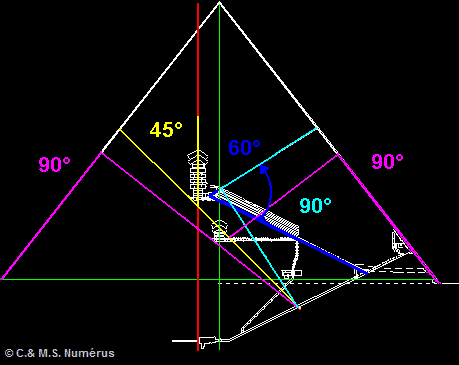
Quid of the very particular angles that one also
could note such as 45°,60°,90° or
perpendicularities between various elements?
Let us examine the geometry of the shafts.
... which are not symmetrical for the King Chambe whose
vertical axis is shifted of 21 cubits but which emerges
appreciably on the same external level.
For the Southern shaft of the Queen Chamber, the robot
Upuhaut measured an average slope of 39 degrees and 60
hundredths i.e. 39 degrees and 36 minutes. The slope of the
external faces of the pyramid is approximately 51 degrees
25. The sum of both would be 90 degrees. Could we
conclude from this that the architectural will was to obtain
respectively perpendicular slopes or that is only the result
of the 7/9 implementation ratio with use of the grids of
construction? (In this case the angle would be of
89° 17 minutes).
But we can especially say that the axis of this shaft
which if it was prolonged would correspond in the same plan
to a point of the great descending shaft that I named "
the Point of Convergence which would be the origin of
the right-angled triangle building report/ratio 7/9.
The Southern shaft of the King Chamber has a slope of
45 degrees. It is not neutral either. If this shaft
were prolonged it would correspond in the same plan to the
same point of the great descending shaft than the Southern
shaft of the Queen Chamber. It cannot be a chance. Even less
if it is noted that this point is straight above the low end
of the Great Gallery. . .
And for the Northern shaft of the King Chamber, which
corresponds to a slope of approximately 33 degrees 30
minutes (ratio 2/3), it will form an angle of 60
degrees with the great gallery which have a 26 degrees
30 minutes slope. (The great gallery was designed by using
the ratio of 1/2 which generates an absolute angle of 26
degrees and 33 minutes).
Finally, the line raised from the point of convergence
towards the Northern shaft of the King Chamber to the
intersection of the shaft with the vertical axis of the
pyramid will form an angle of 90 degrees. (Two axis
using an identical report/ratio, namely 2/3).
The Queen Chamber's northern shaft is not rectilinear and
was only partially explored but seems symmetrical with the
southern one and would also form an angle of 90 degrees with
the external slope of the pyramid. (For this case, it is one
assumption).
Were these so particular values of angles an objective
or a consequence of the method used for the
concept? From my point of view I subscribe to the second
assumption as I will try to show it.
Ancient Egypt perfectly knew the right-angled triangles
and the ratios which govern them as I already showed with
the use of triangles 7-11-13, 11-13-17, 41-53-67.
And although undoubtedly proceeding by means of an
experimental research more physical than theoretical, a
particular property which governs the right-angled
triangles' hypotenuses was necessarily known by them!
I took care to formalize and show this property
which you can consult
here.
By using this property one leads exactly to that
animation shows.
If I also give a report of its existence and of what I
named " the point of convergence " (For the
mathematical demonstration of its
existence, click
here), any architect, site foreman or section engineer
will immediately understand that it is with, and starting
from this type of location, that without the means we have
nowadays, it is possible to control with exactitude the
precision and quality of an implementation by means of
simple aimings!
One will be able to also notice that the intersection of
the great Gallery and the great descending shaft constitutes
another aiming point. he situation of these aimings points
lets suppose that they would have been intended to control
elements primarily located in the Southern volume of
the Pyramid. This also helps to understand that the whole of
the structural components give the impression of a "wave "
starting from North and going up towards the
South.
The numerous mathematical peculiarities of the Pyramid of Khufu are sufficient to demonstrate that they can not be a coincidence but rather that they result from
the knowledge of the designers and methodology implementation
Independently of what you can see on this site (and in particular
"The King's Chamber" 
).
Remember only that ancient Egypt did not have computers and the design still likely their basic tool ...
Clicking here 
allows you to read 11 pages of the book "The Brick of Imhotep" (in French, not translated), which provides you many other different examples about mathematicals results in Khufu ...
|
|
|
| Welcome |
Page Previous |
Top |
Site optimized for 1024 x 768 pixels.
Copyright© C. & M.Sélaudoux 2003-2024
|
|