To give a simple view of my matter, it is enough to know that Babylonians had already search on what later will become " the Pythagoreans triples ".

That is treated in the shelf babylonean wedge-shaped known as" Plimpton 322 " which gather more than fifteen Pythagoreans triples and which are preserved at the university of Columbia, U.S.A

The question of this relation between the numbers continued until our days and Pierre de Fermat did it again on 1621 in its famous conjecture, known as great theorem (or last theorem) of Fermat which states that if n is higher than 2, there are not nonnull entireties x, y and z for which:

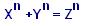
The mathematicians of the whole world during three centuries proceeded to research on this question and at the 19th century a strong reward was promised by the Academy of Science.

The constant of this research during which the pyramids were designed can be read quite simply through the names of all the mathematicians who had has to continue this current, and I will quote among those only some:

After Babylonians, the research continues with Thalès and Pythagore -500 B.C., Diophante of Alexandria -350 B.C., Euclid -200 B.C., Pierre de Fermat, Euler, Gauss until Andrew Willes and, as an example, still nowadays many mathematicians are looking again for the relations between the prime numbers(*).

The Diophante of Alexandria's masterpiece "the arithmetics" comprising thirteen books, as well as the first six books of the "Euclid'selements" were translated on the 16th century, at the university of Heidelberg, by the famous German linguist and philosopher Wilhelm Holtzmann, said Xylander, (1532-1596), then supplemented with accompanying notes in France, in Latin, by Bachet de Méziriac (1621).

Imhotep recognized to be the largest scientist of Ancient Egypt could not certainly be unaware of this question started before him and which continue several thousand years!

(*) Note: Thomas Nicely (Professor of Mathematics Lynchburg College Virginia U.S.A.), is a mathematician who works in the field of the numbers' theory.
He is interested in particular in the field of "twins prime numbers". I.e. with the prime numbers of which the difference worth 2. Examples : 5 and 7, 11 and 13...
On September 1994, He notes that the calculations carried out by one of its computers gave a different result than with other machines.
The involved computer was equipped with the new Intel Pentium processor.
The mathematician discovers that this new processor Intel Pentium gave an incorrect result during the calculation of 1/824633702441.
(This number appeared in its calculations for 824633702441 and 824633702443 which are twins ).
Thus was discovered and communicated the " Bug " of Pentium on October 19th, 1994.

Welcome	Page Previous	Top